Now that I have finished an overview of what spells have in common, we can talk about specifics - individual magical effects that make up the rest of the magic system. I will start by talking about temporary objects - a key to understanding many summoning and creation spells.
As usual, if you are confused about any terms, make sure to check out the glossary, and if you are looking for other posts, check out the blog map. I would also like to thank Augsphere and Verglasz for various help on this article.
Let’s start from the beginning. What do I mean by temporary objects?
Many spells (Summon Instrument, Summon Weapon, Summon Monster, etc) create an object that is temporary - after the spell runs out, the object disappears. Until it does, it behaves like a normal object in all respects. There are two broad sets of questions when it comes to this class of spells.
First one arises when you consider what would happen if the summoned object was significantly changed while the spell was still in effect. For example, if a summoned creature (e.g. from Mount) is eaten, does it provide sustenance? Can you melt down a sword produced by Summon Weapon and make something else out of it, if you are really quick? All of these questions can be answered by defining how the constituent temporary matter behaves while the spell is in effect.
Second set of questions comes from the realization that making objects show up should have all sorts of side effects. For example, if you cast a summoning spell into a box that is too small to contain the summoned object, does the spell fail or does the box break down? Is there a vacuum clap every time duration runs out on a summoning spell, and the object vanishes, leaving behind nothing? Laws concerning creation and destruction processes of temporary matter provide an answer here.
To answer both of these sets of questions, I present an ectoplasmic theory of summoned matter. Let’s begin by considering what the temporary objects can be made out of.
1. No-matter models
The first model I would like to mention says summoned objects aren’t made out of anything. Instead, they are merely constructs (e.g. made out of force) with weight and colour. A set of additional rules determines how these constructs behave when bent or otherwise deformed, and what circumstances lead to a complete collapse of the spell.
I think this is a poor model, and would not talk of it further. The problem isn’t so much that you couldn’t make this model work, but rather that the complexity of these additional rules explodes very quickly when you look at it closely. The set of properties physical objects have is simply too large. Here is just a small sample them:
Weight
Moments of inertia
Surface texture
Sound propagation
Elasticity
Heat propagation
Heat capacity
Major vibration modes
Electrical conductivity
Surface chemical interactions
And while I one hundred percent believe you could make all these properties fit without using atoms, I think the resulting model would be far too complicated.
2. Ectoplasm
A much better model uses what I call “ectoplasm”. Ectoplasm is a form of matter that constitutes temporary objects. It has two phases. Here phase is used much like in physics - some state for the material with distinct properties, e.g. ice/liquid/vapor for water.
In the first phase (pure ectoplasm) ectoplasm has the consistency of water, is chemically inert, and does not mix with regular matter: if stirred in, it would form an emulsion instead.
Phase transition from the first phase to the second phase is going to be called “snapping”, and will involve ectoplasm transforming into normal matter - atoms and all. The second phase is thus called “snapped ectoplasm” or “ectoplasmic matter”. The only distinguishing feature between ectoplasmic and normal matter is that the former has a little value attached to it, saying how long it will last until disappearing, and which spell it belongs to. Because we want arbitrary objects to be summonable, ectoplasm should be capable of snapping into arbitrary atoms.
Given this two-phase model for ectoplasm, we can sketch out a step-by-step algorithm for how the summoning spells behave:
Spell determines the “map” for ectoplasm: specific locations in space are associated with specific resulting atoms. This may include checks that the target object will fit into the surrounding space, and a failure of the spell if it cannot.
The question of how the spell selects a specific area has already been discussed in my overview of the general spell properties, under spatial selection. How the spell maps atoms onto this area will be discussed in a later post.
Ectoplasm is generated and fills in the object boundary, pushing away the surrounding liquid or gas.
Ectoplasm snaps, and we now have a summoned object.
Object is used and deformed in various ways; it behaves exactly like normal matter should. As a result, ectoplasmic matter is moved around.
Once spell duration runs out, ectoplasm disappears, wherever it was, in a reverse of the snapping process.
Dispelling is treated as a premature start of the unsnapping process
3. Bubble model of ectoplasm manifestation
Proceeding chronologically through this list, let’s discuss how the process of filling in the object boundary works. Two key things have to happen, in order, for the boundary to be filled. First, some amount of ectoplasm has to be generated. Second, if that ectoplasm wasn’t generated exactly at the target location, it has to move to the target spot. This process would repeat until the entire boundary is filled. A good way to visualise this is to imagine ectoplasm being blown like air bubbles from a cocktail straw, before being shepherded to their target location, and joining with other bubbles into a larger bubble.

Three key variables control the creation of ectoplasmic bubbles: surrounding pressure, presence of nearby objects, and target bubble size. Generally speaking, there is no need to determine the latter parameter, other than to say it should be smaller than characteristic features of the summoned object. Former two parameters are more interesting.
First of all, as the bubble expands from size zero to the target size, it has to overcome the pressure of the surrounding environment. In principle, we can introduce a maximum allowed pressure, above which ectoplasmic bubbles can’t expand and the summoning fails. See section 10 on why this may be desirable. This would also introduce a depth limit to summoning spells: every 10 meters of water are equal to one atmospheric pressure.
Secondly, such a bubble can’t be created within any solid objects, or press against them during creation. This limit is in place to make sure we do not damage the environment during the summoning process: it’s trivial to show that if a bubble can overcome the pressure imposed by 10 meters of water, it can also easily crack solid objects if it appears inside of a narrow crack.
We thus have minimal requirements for the bubble creation: no objects being closer than the bubble radius to the source point, and environmental pressure being below a critical threshold.
4. Bubbling behavior
Splitting ectoplasm into bubbles also presents a neat pressure control mechanism when creating objects with voids inside of them (e.g. various containers). With other models, it’s hard to say what would prevent the summoned object from “squeezing” a lot of the surrounding medium into the hole, leading to dangerous levels of pressure, and an explosion once the summoning concludes. Bubbling ectoplasm model avoids this: ectoplasm has no inherent shear strength, and so the extra matter can simply “bubble out” of the area before the snapping starts.

If the target object boundary is free from all external objects, then bubbles can be created exactly where ectoplasm is not yet present, and very quickly merge with other nearby bubbles. If that is not possible, then bubbles could be created outside of the target area, and move to an “unoccupied” position. In the process, they would push at objects, moving the spell area as described in spatial selection type 3, “Expansion from a movable target point while preserving shape”.
This push comes from a requirement to conform to Newton’s third law, as I’ve described here in a relativity section. In the case of summoning spells, the ectoplasm bubble is anchored to the spell itself: thus if the spell tries to push the bubble into a wall, then the spell will be moved backwards, increasing the viable area for ectoplasm manifestation.

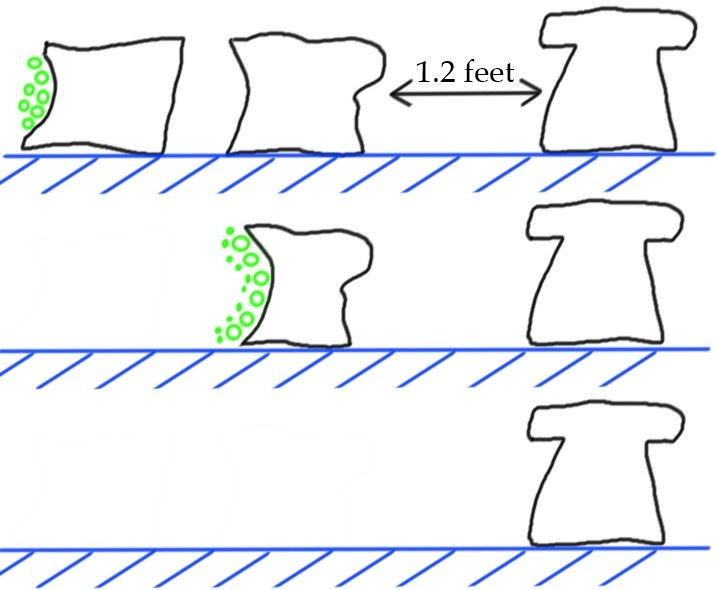
This process is easiest to explain with a picture. Let’s look at the diagram on Image 3.
Top left: a dagger is attempting to manifest. The handle is completely filled with ectoplasm, while the blade is inside of the wall and can’t be manifested. Center of the target area is shown as a red cross. Forces acting on the ectoplasm bubbles (trying to push them into the wall) and on the spell (pushing it away from the wall) are shown as red arrows, and the total sum of the forces is naturally zero in accordance with Newtonian laws.
Top right: because of the force acting on the spell, the spell and the target object boundary are moved away from the wall.
Bottom left: because the target object outline was moved, previously manifested ectoplasm is now in the wrong place. This is easy to see on the guard of the dagger. That ectoplasm can either move with the target area (imposing more forces on the spell, same way that a swimmer’s hand imposes forces on their body by pushing on the water), or simply vanish in the previous area and manifest in the new area (as shown on the picture). Here the zone of vanishing ectoplasm is outlined in violet.
Bottom right: Dagger’s handle has now reached the other wall. Now two sets of pushing forces are imposed on the spell, balancing each other. The spell will not move anywhere and the dagger will be stuck in a half-manifested state. If it is not balanced perfectly, it is likely that the forces will impose a moment on the dagger and slowly rotate it out of position until it can manifest fully.
A canny reader would ask about the magnitude of the pushing forces involved: will this pushing process move other objects around, or damage them? Fortunately, this magnitude doesn’t have to be large, because mass of the spells themselves can generally be assumed to be small; for the sake of consistency, I think using the same magnitude of force as used for tests of object solidity (i.e. equal to bent pinky finger) should be fine.
In that post, I left the exact value of the testing force undefined. Now we can specify it: doing some tests with a kitchen scale, I get a value of about 10 grams for the force imposed by a bent pinky finger; that is also comparable to the weight of coins one can hold on their pinky finger without stressing it at all. Converting this into pressure, we get a value of approximately 4000 pascals, enough to lift about 4 kilos when applied over a surface 10 by 10 centimetres wide, or 400 kilos when applied over a square meter. You can see the effects of even slight pressure lifting objects here.
This pressure is a bit too much for my taste; it would move even fairly large objects around (e.g. people, cupboards) when summons attempt to appear in enclosed spaces. To combat this problem, we can simply reduce it proportionally to the size of the area in contact with other objects. That way the total lifting force on all the surfaces the summoned object is pushing on is kept equal to the aforementioned bent pinky finger.
Formulating pushing forces in terms of pressure gives us an easy way to judge which way the spell will be trying to move: specifically, away from the largest cross-sectional area where the target object boundary intersects with nearby objects.
Certain spells (e.g. Ice Spears) instead use spatial selection type 2 with a larger force (in case of Ice Spears, 4000 pascals is actually in the right ballpark - assuming the spears start with an area of one foot by one foot, it would be enough to lift 36 kilos - more than enough to trip people), in order to move their targets around. An appropriate value would depend on the specifics of the spell.
5. Snapping progression
While you can imagine many ways in which the snapping can progress (from the outside in, from the inside out, from random points, etc), differences between the methods would be mostly cosmetic and won’t play a huge role. Furthermore, if you do encounter a situation where differences are important, I think it should be trivial to figure out how it should be handled, just by carefully considering what is happening.
Instead, a much more interesting consideration is wherever the entire object boundary has to be filled out for the snapping to start (full snapping) or wherever snapping starts at certain locations before others have been filled with ectoplasm (partial snapping).
Core difference between these two methods is what happens when surrounding space can’t fit the entire summoned object. For full snapping, you naturally need the entire boundary to fit within the surroundings, otherwise snapping can’t take place. On the other hand, for partial snapping, this isn’t necessary. It should be possible to summon an object into a location that can’t fit it entirely: only a part of the object would materialize, with the rest of the object being blocked by walls. If the walls are removed, the rest of the object may materialize, or it may be stuck in a partially materialized shape. For a look at how this could look like, look into the previous section, and simply replace ectoplasm manifestation with snapping.
Overall, I prefer partial snapping: it gives magic some pretty interesting flexibility. Full snapping, on the other hand, is “safer” in terms of unpredictable side effects. A potential middle-ground can be partial snapping with a minimum fill percentage: for example, at least 90% of the object boundary should be filled in beforehand.
6. Unsnapping, dispelling and object locality
Having discussed the creation mechanism, we can talk about the opposite - the destruction mechanism, which I call unsnapping. One of the main concerns during destruction is preventing vacuum pops - if the object were to disappear instantly, then the space previously occupied by it would be filled with vacuum, and would collapse with a gunshot-like pop.
In order to prevent implosions the disappearance process is deliberately slowed down in order to give the environment some time to fill the newly freed area. I call the model used for this “unsnapping waves”. You can imagine them as crystallization waves going through some supercooled water, except instead of turning into ice, water turns into nothing. Disappearance process then involves such waves starting at the surface of each part of the summoned object and proceeding inwards, until the object is fully gone.
Mechanics of these waves can be made to be very reductionist, using just two simple rules. First of all, any piece of ectoplasm one foot away from another piece that had just unsnapped unsnaps as well a short time (e.g. 30 milliseconds) later. Second, when spell duration runs out, small patches of the material on the surface of the object unsnap. These two rules together produce the wave behavior we want, with the unsnapping delay determining the effective wave speed.

This slow down doesn’t actually affect the base mechanics of the spell much. Let’s say that we have summoned a big ship that we can approximate as a cylinder 20 meters in diameter. If disappearance takes half a second, then the surrounding matter only has to move at about 20 meters per second (radius of 10 meters over half a second) to fill the void. Winds of this speed are a 9 on the Beaufort scale; dangerous, but overall tolerable, especially since they will be gone in half a second. Most importantly, there is no crack or implosion. For objects smaller than a ship, there would be barely any noticeable wind.
Unsnapping waves is also the model I use for dispelling. Dispelling spell simply causes a small patch of the material that it touched to unsnap, provoking an unsnapping cascade, and making the object vanish.
Distance of one foot used in the definition of unsnapping waves is used to decide which parts of a dispelled object unsnap - due to locality assumptions, this is the only way I can see to handle summoned objects made out of different parts (which can be separated by an arbitrary distance) within the context of our locality assumptions.
Note that unsnapping waves do not remove the possibility of vacuum implosions entirely, they simply minimize it in the vast majority of circumstances. For example, if you have an ectoplasmic object that is sealed inside of a real object, you may end up in a situation where there is no nearby environment to fill the void, thus forming a vacuum. However, such tight seals should be relatively uncommon.
7. Matter replacement vs matter movement
There is an assumption I have made in point 3, that has so far not been interrogated, and I think it’s time to address it now. This assumption is that the summoning process pushes the matter that was previously occupying the object’s space away.
An alternative model would be to say that the matter is replaced: no actual movement happens, and no pressure equalization is necessary. We simply select a region of a liquid or a gas, remove everything inside, plop in our summoned object, and we are done. Once the spell duration runs out, we either replace the object with the original matter, or we use the same algorithm as in point 6 to prevent a vacuum pop. If the latter algorithm is used, then the original matter is simply gone.
While this would be a viable spell model, I do not like it for one simple reason: this is no longer summoning, this is transmutation. Summoning spells should actually summon objects, making something entirely new show up, instead of doing a sneaky in-place substitution.
There is no logical reason why transmutation couldn’t be used to achieve the same effects as summoning spells. You would naturally have to track what matter was used to originally create the “summon”, and handle its re-deposition when the “summon” disappears. This could lead to some interesting consequences - e.g. you could use “summons” to move original material around, in particular if you wanted to use something explosive or poisonous as the “summon” basis, in order to have a secondary effect once the spell duration runs out. But transmutation is a different magical effect, and as such, will be covered in a separate post.
8. Permanent summoning
Not all summoning spells conjure temporary matter; some conjure permanent matter instead. Fortunately, there is no need to discuss them, because permanent conjuration is mechanically a subset of temporary conjuration. The only main difference is that it can’t be dispelled, and does not need to deal with unsnapping: snapping mechanisms should all work largely the same.
8.1. Inconsistencies in spell texts
Magic chapter of the rules states “If the spell has a duration other than instantaneous, magic holds the creation together, and when the spell ends, the conjured creature or object vanishes without a trace. If the spell has an instantaneous duration, the created object or creature is merely assembled through magic. It lasts indefinitely and does not depend on magic for its existence.” You would think that this would be a good way to differentiate temporary and permanent conjuration, but it isn’t, because some spells don’t agree with this definition.
For example, Pellet Blast is Instantaneous, but explicitly states pellets disappear at the end of the spell. Create Water is allegedly instantaneous, but disappears after 1 day if not consumed - meaning it obviously can not be permanent.
My position on this is that you should read the text and intention of the spell before deciding whether it’s temporary or not, and that water created by Create Water should not disappear after a day, because that will simply lead to a huge mess of edge cases.
8.2. Disintegration spells
Spells such as Disintegrate, as well as spells that use permanent removal of matter as part of their functioning, can be seen as simply unsnapping of permanent matter, and so should obey all the same rules.
8.3. Conditional permanency
When it comes to some spells, it may be useful to think of them as summoning conditionally permanent matter. For example, Create Water may be creating ectoplasmic matter that becomes permanent when it is consumed by a body that is occupied by a soul (read: enters the same space as an occupying soul). This is a way to cut short most (though not all) murderous effects summoned matter has on biological creatures.
Similar effects can be imagined for other relatively simple physical conditions. Overall, I dislike introducing such conditionality. It overcomplicates things, isn’t necessary in 98% of cases, and frankly, I just like summoned matter killing you in 13 different ways if you try to eat it.
9. Cups, balls, and probability
Before we can finally start discussing the consequences of this magic model, we need to talk about one last key element. And for that, we will need to dip a bit into quantum mechanics. Don’t worry, there won’t be any math, and if you are still feeling uncomfortable, you could skip this section. This isn’t going to be very rigorous anyhow.
Quantum mechanics is famous for being hard to understand, but in my view that difficulty is one big myth, perpetuated by decades of abysmal teaching of the subject. It’s no more difficult than any other part of physics. If you would like to learn some, I hear that Quantum Computing Since Democritus by Scott Aaronson is good, though I haven’t read it myself. What I have read is Feynman’s Lectures in Physics, which I very much recommend. In principle, you can use any other learning material, up to and including lectures on YouTube; just make sure to skip any that start by giving a long spiel about how impossible to understand quantum mechanics is, or ones that go on an overview of every historical experiment and “paradox” that lead to the development of the modern theory; those won’t teach you anything good and will just confuse you endlessly.
For now, all you will have to know about quantum mechanics is this:
There is no way whatsoever to differentiate between two particles of the same type, such as between two different electrons. If I show you an electron and ask what atom it came from, there is absolutely no way for you to know that, no matter what information you have at your disposal. In fact, if there was such a way, even in principle, lots of things such as electron bonds between atoms would instantly stop working.
Instead of having concrete positions, all particles are smeared across space. All that you have is a cloud of probability where you may get an interaction with that particle.
Most of quantum mechanics has to do with mathematical rules for how those clouds of probability move, interact, and change, which we will not get into here.
The core problem with our definition of ectoplasm is that it breaks rule 1: currently, it is possible to distinguish temporary and permanent particles. This is a big problem, and so we have to fix it without modifying the overall behavior of what I have described previously.
To solve this problem, let’s first abandon any hopes of telling “temporary” particles apart from “permanent” ones based on inherent properties; instead, we will try to keep track of where we put new particles, follow them along to where they end up at the end of the spell duration, and pluck them from there. That, in itself, seems very difficult: given that there is no way to tell them apart from other particles, and that they don’t have a specific position, how could we possibly keep track of them? It’d be like trying to keep track of a specific needle in a bucket of needles that was constantly being shaken and mixed, all the while our vision was extremely blurry.
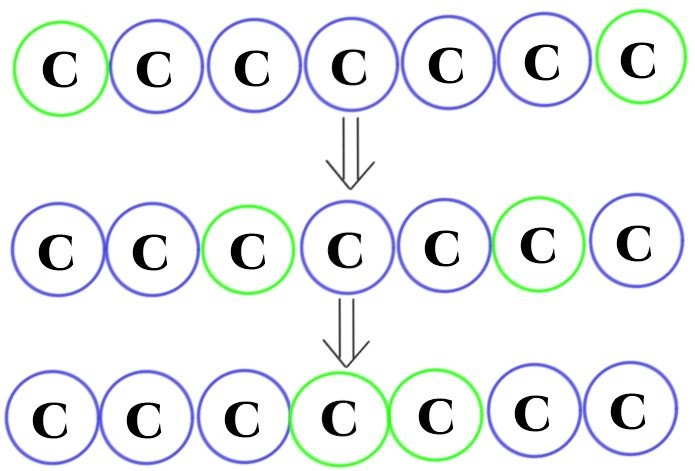
The solution I propose is what I call the cup-and-ball mechanism, named after the famous cups and balls magic trick. The basic principle is that we don’t try to keep track of where the “temporary” particle is, exactly; this is impossible, just like it’s impossible to keep track of the ball while it’s under an opaque cup. Instead, we try to keep track of the cups themselves, which in the case of quantum mechanics look like smoothly moving regions of high likelihood to find our particle, starting from the location where we added them into the world.
If our particle gets close enough to others of its type and gets into an interference pattern where we can’t tell the two probability clumps apart, this is fine: we simply assume that either of the particles could be “our” one with a 50% probability, and act accordingly. If the particles later split up and interact with yet more particles, we split probabilities further, so that with three potential candidates we might be looking at 50/25/25 odds. At the end of the spell duration we roll our metaphorical dice and pluck one of the particles out of the universe.
Thus instead of having an electron that is ectoplasmic, we will have a region of space where we know that one electron should be removed. You can call this “ectoplasmic charge”. In most cases, there will not be a difference, so I will use the terms interchangeably.
Finally, I will introduce a rule that says that these regions attract one another. If we have a series of particles of the same type, and two of them are ectoplasmic, ectoplasmic charge will jump between particles until it’s close together. Frequency of such jumps would be inversely proportional to the mass of the particles, such that atoms heavier than lithium experience very little drift.
The main reason for this rule is prevention of certain high-energy reactions that don’t seem to be present in DnD magic. First example of such a reaction has to do with electron clouds.
9.1. The electron problem
Let’s say that we attach ectoplasmic status directly to the particles with no drift. With electrons, this causes the world to blow up.
Let’s say that we have summoned a length of copper cable - for example, a meter long and a square centimetre in cross section - and attached it to more cabling that is not ectoplasmic. Then let’s say we ran some current through the system, until we were sure that all of the summoned electrons left the summoned length of cable. Then, we will wait for the spell to run out. After it does, we will have a length of cable that is highly positively charged (where all the summoned electrons were and disappeared), and a void in space filled with electrons (where our summoned copper was).
Now, when I say highly I bloody well mean highly. Copper has ~8e28 free electrons per cubic metre; this means ~8e24 of them for our cable, for a total charge of 1.3 million coulombs. That’s a lot of coulombs. Doing some back of the envelope math for the potential energy of our system of charges here, it should be at least 1.5e22 joules - comparable to the Shoemaker-Levy collision with Jupiter, or about 5 times the total energy of the last Yellowstone supervolcano eruption.
And it’s not like we are reaching the limits of potential energy generation - we could very easily have one hundred such cables running in parallel, for one hundred times the released energy. That would easily get us to energies released during the asteroid impact that killed the dinosaurs.
All of this is prevented with ectoplasmic charge drift. Due to the very low mass of electrons, their ectoplasmic charge would keep jumping backwards through the current, never leaving the atomic cores, and thus never generating abnormal charges after the spell ends.
9.2. The water problem and hydrogen exchange
Next large issue prevented by ectoplasmic charge drift has to do with hydrogen exchange. Hydrogen atoms are constantly being exchanged between different molecules containing hydrogen; this can be easily seen when some hydrogen is replaced with deuterium. Rate of exchange can be measured by measuring the weight of molecules, and it turns out to be very very high.
It is also the reason why water has anomalously high electrical conductivity. Normally, liquids conduct current by moving ions around, which is relatively slow because they need to physically move within the solvent. You also need a lot of ions to carry all that current. In water, hydrogen atoms don’t move as much as get shuffled along a chain of water molecules, in what is known as the Grotthuss mechanism. This is easier, and so conductivity is higher. However, this exact drift is what causes problems for summoned water.
Let’s say that we have one liter of normal water and one liter of ectoplasmic water. We mix them, and let them reach equilibrium. For any given molecule, we have a 50% chance of the oxygen atom being ectoplasmic, and a 50% for any of the two hydrogens being ectoplasmic. We would thus have the following breakdown of molecule variant and recombinant concentrations:

Let’s look at just the OH and H compounds here. They recombine to form water; this reaction releases ~500 kJ/mol energy due to the extreme reactivity of the compounds (H enthalpy 218, OH 37, H2O -241 kJ/mol). In two liters of water, we would have 27 moles of OH and the same amount of H, and so 13.5 MJ of energy would be released. To heat one liter of water from 0 to 100C requires only 0.42 MJ; to evaporate it into water vapor, 2.2 MJ; to heat that vapor up to 600 C, another MJ. We can thus see that the energy generated by our recombinants after unsnapping will be more than enough to vaporize the one kilo of matter we have had initially and make it violently explode.
This would seem to present a problem, because in DnD, water does not seem to explode if it has been mixed with temporary water at some point. Fortunately, this kind of exchange seems to only be a significant problem with hydrogen, probably due to its low mass and poor bonding strength.
Ectoplasmic charge drift prevents this problem from appearing, as it will skew the ratio heavily in favor of fully ectoplasmic water molecules due to ectoplasmic charge of hydrogen moving to water molecules with ectoplasmic oxygen. Some radicals would still form - that is inevitable when it comes to statistical laws - but as long as their concentrations stay marginal, their presence will not affect much.
10. Pressure, eardrums, and the shark-busters
Now that we have outlined all the basic laws of physics when it comes to ectoplasm, let’s discuss some consequences of those laws. First of those is the impact of summons on the surrounding pressure.
Our ectoplasm bubble model successfully evades a lot of problems related to summoning, but there is no way to evade one simple fact: any summon takes up some volume that was previously occupied by air or water, and so this air or water has to be pushed out of that volume during the summoning process. In an enclosed space, this inevitably leads to an increase in the surrounding pressure.
Degree of pressure increase depends primarily on two things: how large is your summon compared to the local environment, and how tightly the local environment is enclosed. Summoning when under the open sky is pretty much never going to be a problem; on the other hand, summoning an elephant inside of a tightly sealed room will blow out your windows for sure.
When considering this issue it is useful to put things into terms of overpressure. Overpressure is a term commonly used to refer to blasts from explosives, and refers to pressure of the blast above the atmospheric pressure. Summoning happens too slowly for any blasts, but it does nonetheless create pressure above what was present previously: I will use the word overpressure to refer to this increase.
The reason overpressure is a better measure than the total pressure is that human bodies and most objects in the environment adjust easily to very different levels of pressure. For example, human bodies can operate with no issues one hundred meters underwater - at a depth where pressure is more than ten times the atmospheric. What is damaging, on the other hand, is the pressure difference between different cavities.
Before summoning happens, everything in the environment is likely to be at atmospheric pressure. Summoning pushes away air, thus increasing local pressure within some enclosed space - for example, a room with closed windows. Indirect damage from the summoning will thus depend on overpressure in this room compared to atmospheric - because that’s the pressure difference now acting on your eardrums, the windows of the room, and your chest until it has a chance to equalize.
10.1. Pressure damage
Before we get into how overpressure could be generated, let’s shortly discuss the main effects it has on the environment and on humans.
<700 Pa, <1% of atmospheric pressure: this level of overpressure should have no effect on anything of importance. It would generate drafts (strength depends on how tightly the windows are closed in the summoning room), but other than that, it would not be noticeable.
700 - 900 Pa, >1% of atmospheric pressure: According to this article, this is a typical pressure limit of residential windows. Of course, this refers to overpressure: how much pressure wind can put on the window from one side in comparison to the other. Going above this limit may not shatter your windows (after all, designers probably put in a safety margin), but it just as well might.
1.8 - 2.6 kPa, ~2% of atmospheric pressure: According to this article, your ears pop about every 500-1000 feet (150-300 meters) of altitude. This translates to a pressure difference of about 2000 pascal, as you can verify with this pressure calculator.
35 - 100 kPa, 30-100% of atmospheric pressure: At these overpressures your eardrums burst; what exact pressure is needed depends on individual variability of different people. Likelihood that rupture occurs seems to increase linearly in the log of the overpressure. A ruptured eardrum leads to a high chance of hearing loss, though often they heal on their own within a few weeks.
100+ kPa, 100%+ atmospheric pressure: People start to die from lung trauma. Exact values differ from one source to another, and are based on case reports. Unfortunately, ethics boards tend to frown on the suggestion of deliberately exploding people as part of an RCT trial. This is further complicated by the fact that values such as the duration of overpressure and rate of pressure rise are very important in deriving the lethality of the blast.
According to “The Effects of Nuclear Weapons. Third edition” by Glasstone and Dylan, 1977, duration of overpressure is not important as long as it’s longer than 100 milliseconds; I think that this would be the case for all practical cases of summoning overpressure. Summoning generates pressure by a relatively (compared to explosions) slow expansion of the summoned matter; this means the surrounding medium should have plenty of time to evacuate the area, resulting in low overpressure most of the time. The only case where overpressure would be high is if the surrounding space is reasonably hermetic and can withstand the pressure - in that case overpressure should logically be present for at least 100 milliseconds.
As far as the rate of pressure rise is concerned, I have not managed to find any good data on which rates are lethal and which ones aren’t. Explosions are much quicker than summoning, so the data from them is not applicable. You would think that there would be data on de- or re- pressurization accidents, such as maximum descent rates in water, but I can’t find any data. We know that increasing the surrounding pressure by one atmosphere over ten seconds is biologically fine; we also know that increasing it over 10 milliseconds is not fine. Summoning is in a frustrating gray area where no data is available and it’s plausible that the question could go either way. So, let’s make an unfounded logical leap. We know that a time of 100 milliseconds is long enough that further increases in overpressure duration do not increase damage. We can thus surmise that there is a certain effective “reaction time”, some sort of “inertia” to your tissues, bones, lungs and such, on the scale of 100 milliseconds. We can then make a leap and say that this is also the critical time for determining the pressure spike for the purpose of lung damage. Maximum pressure change over any 100 millisecond window would then be the critical damage indicator, which you could compare to the overpressure levels above.
10.2. Overpressure model
To calculate overpressure caused by summoning in air within enclosed spaces, I coded up a little calculator in google sheets. It assumes that we are summoning some object within an enclosed room, and that this room has some holes (e.g. windows, cracks under doors, etc) through which air can escape into the surrounding environment.
If tinkering with a calculator is not for you, or your case is more complicated than what I designed it for, you can rely on a simpler model that assumes no outflow whatsoever. This should provide you with an upper bound on the overpressure you would see.

Calculator should be relatively user friendly - to get a pressure graph for your use case, simply copy the sheet, fiddle with the parameters (blue cells), and google sheets should do the math for you. Don’t edit the calculations sheet, as that’s the part that does the math magic.

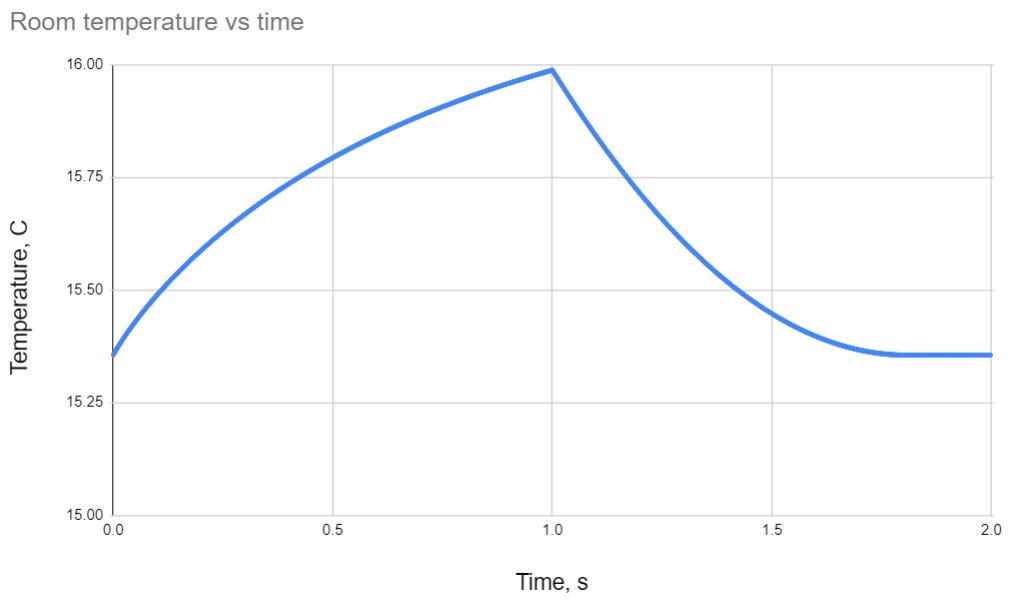
I decided to test the calculator by assuming a small room (4 by 4 by 2 meters), and a fairly large object (half a cubic meter, equivalent to a ~500 kilo horse. Nice thing about the metric system is that you can convert from kilos of flesh to liters directly, because it is all about equal to the density of water...) being summoned inside. This room also has 0.012 square meters of holes, which you can imagine as millimetre-wide gaps alongside the door (1.8 by 1 meter = 5.6 meters perimeter = 0.0056 sq meter outflow if gap between the door and door frame is one millimetre) and a couple closed, though not well-fit windows (1 by 1 meter window = 4 meters perimeter = 0.004 sq meter outflow). As you can see from using the calculator, pressure increase even in this fairly well-enclosed room isn’t sufficient to blow the windows out. This means that generally speaking, summoning should be completely safe if you crack open a window. Larger rooms would likewise make this problem go away.
One interesting feature is that due to air compression, air heats up by half a degree, and then cools back down as the extra air escapes out of the room. This, as well as the pressure spike, can be used as an entirely non-magical method of summoning detection.
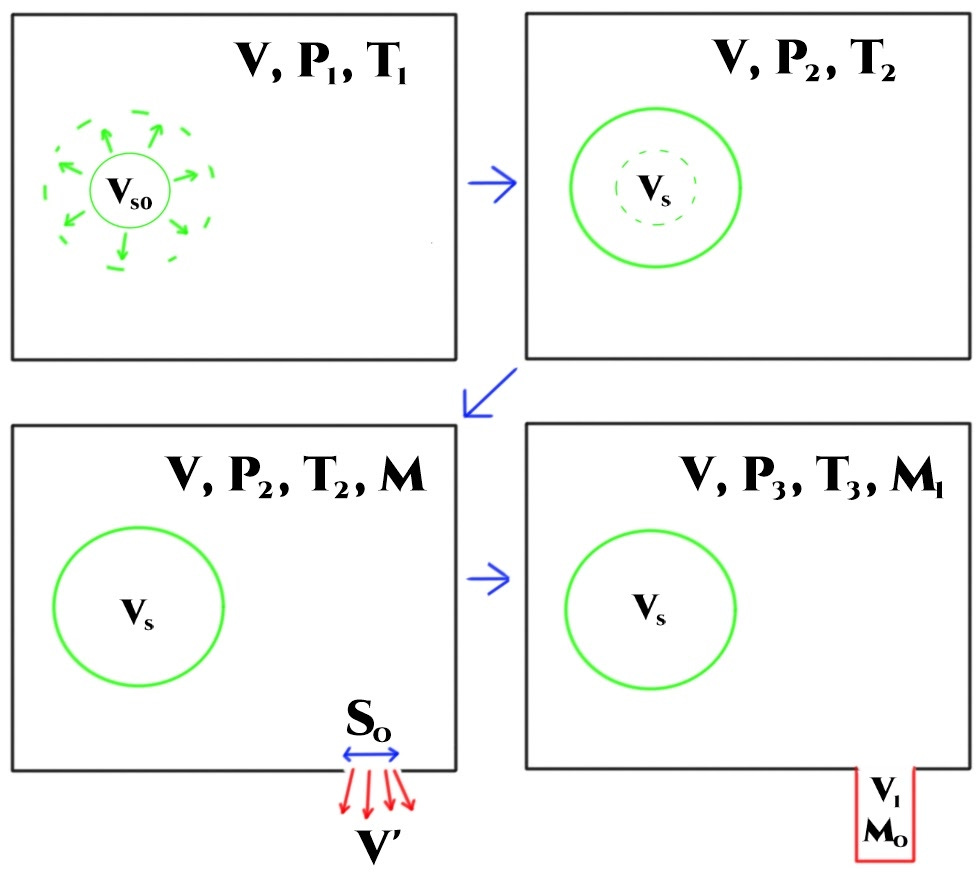
I think it is important to explain the model I used to make the calculator, so the rest of this section will deal with that. If you aren’t interested in the physics of it, feel free to skip it.
Calculation itself is actually fairly simple, and utilizes an iterative algorithm to approximate the physics. It consists of two steps that are repeated one after another. First, I assume that the room is completely sealed and has no openings. I then calculate how much the pressure would increase over some miniscule period of time (timestep) from the increase in the volume of the summoned object. I assume that this is a relatively fast process, so pressure increases adiabatically.
Then, I calculate the outflow speed of air using Bernoulli’s equation.
Finally, I imagine that the room expands a little bit, in such a way that the mass of air inside of the marginal increase in volume is equal to the mass of air that escapes the room over the duration of the timestep, using the outflow speed I calculated in the previous step. This is used to model air escaping out of the room. I likewise assume this expansion to be adiabatic. I then calculate the pressure inside of the new expanded room, throw out the expanded volume, and start over with the first calculation step. All of this math is repeated for every time step, of which there are 2000. As a result, we get a nice smooth graph of overpressure inside of the room.
Looking at the images above, you can see all the parameters required for making our model. Here are the explanations for what they refer to:

Now that we have all the necessary parameters outlined, calculations for every timestep are fairly trivial.
First step is an adiabatic compression of air, which is treated as an ideal gas. Therefore we can use the polytropic process equation (1) to figure out the invariant. For air, gamma (2) is equal to 7/5 exactly. Substituting pressures and volumes for two states we have, we get relation (3), from which we can get pressure after the compression step (4). Volume of the summoned object is assumed to change linearly, so after a single timestep it is equal to (5) where K is a constant depending only on the final volume and how long the expansion process will take. We therefore know the values of all parameters on the right side of (4), and can calculate the resulting pressure.
Using Mendeleev-Clapeyron ideal gas law (6), we can calculate the temperature of the gas after this compression (7) which is used purely for graphing purposes. Using a reduced form of the Bernoulli equation (8) we can also get the speed of the gas flowing through the gaps in the room (9).
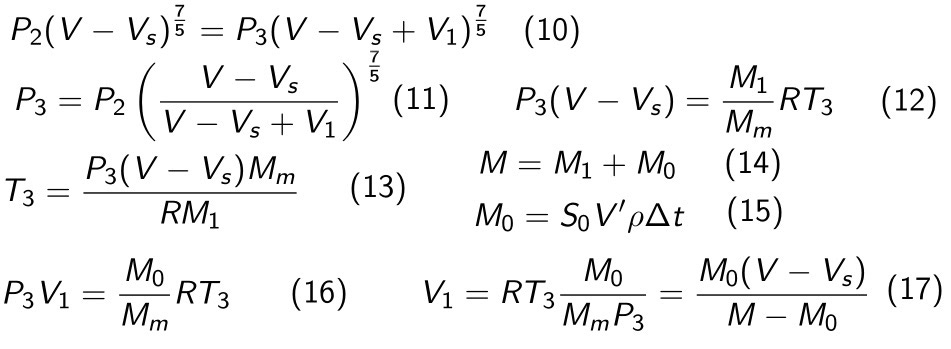
Largely the same process is used for the second calculation step. First, we substitute two respective states into (1) to get (10), from which we get a formula for the pressure after the final calculation step (11). In order to use it, we will need the volume of the fictional “extra” space added to our room. We first apply (6) to our larger room in order to get (12), from where we can find the temperature of the air after the second step (13). Masses of the air in the larger room and in the additional smaller one should sum up to the mass of the original air (14), and the mass of air in the additional room can be calculated from the outflow velocity and the density of air (15). We then apply (6) to the extended space to get (16), from where we can calculate the volume of the fictional space (17) using the temperature we derived in (13). This can then be substituted into (11) and be used in calculations directly.
I make some major assumptions in my modeling, which may be misguided. Pressure increase is assumed to be adiabatic, which is not actually true except approximately, and not true at all if there is significant heat exchange with the room. Expansion of air during outflow uses a sketchy volume expansion substitute, which I am not hundred percent sure is true even approximately. Bernoulli equation is used to model air escaping; I thus implicitly ignore both viscous effects (significant in thin gaps, choking the flow further) and turbulent effects (significant in wide gaps and at high speeds, also choking the flow). Pressure is assumed to be equalized within the entire room and to be constant on the outside - probably true for summons that take up a small part of the room’s volume, but I am not sure if it’s going to hold up if you summon something 2/3 the volume of the room. Density of air is assumed to be constant and not depend on pressure - assumption which shouldn’t affect much because changes in density would be a second-order term which I ignore anyways - but is still important to keep in mind.
Overall, I think all of these assumptions are mostly justified and the calculator is usable, but I wouldn’t be surprised if it gives wildly inaccurate results if you use it for extreme situations.
10.3. Underwater
Model I described in the previous section is applicable to air, as well as other gaseous environments. In water, overpressure spikes much more quickly, because water is much less compressible than air.
You may have heard that water is incompressible. This isn’t true: for example, water at the bottom of the Mariana trench is about 5% denser than on the surface, because it is compressed by the immense pressure. However, it’s true that water compresses very little. As a result, even slight variations in volume of an enclosed vessel filled with water will lead to very large changes in pressure.
Let’s put this in context. Say you are summoning a shark inside of a fairly large enclosed body of water - for example, a tank or a cave 20 by 20 by 20 meters. To give you a visual, it would be a cubic tank as tall as a 6 story building. Volume of a big shark is about 4 cubic meters. Volume of our vessel is 8000 cubic meters, more than double of the volume of water in the shark exhibit at the New York oceanarium (800 000 gallons ~ 3600 cubic meters). Volume change would thus be just 500 parts in a million.
Bulk modulus of water is such that a decrease of volume by 46 parts in a million leads to an increase in pressure by one atmosphere; this means that after you summon the shark, pressure inside of our tank would spike by about 11 atmospheres. This is an equivalent of going from the surface of the water to 110 meters deep over the course of a second. Over a 100 millisecond window, this is about one atmospheric pressure, equal to 14 PSI: more than enough to kill you.
As another point of comparison, there are people who compete to dive as deeply as possible on a single breath: free-divers. One of the world records in this sport is 145 meters. The diver starts his descent at 1:17, and reaches the bottom at 2:30, so the entire descent takes 73 seconds, for a descent rate of ~2 meters per second; this dive required months of preparation, and if they could have made it faster they probably would have. Our “effective descent rate” would be 50 times as fast.
This is all assuming our vessel has no way for the water to go and manages to contain the pressure. If there are ways for the water to flow out (for example, because there is air above the water, so it can rise), then the pressure will not increase nearly as much; refer to air calculations on how the pressure of the air would increase. Likewise, most containers are not built to handle a pressure of 11 atmospheres, let alone a sudden increase to that value. Whatever walls there are, they would likely crack at their weakest point, letting the water out, and thus preventing the pressure from ramping up quite as quickly and to the same maximum values.
As I mentioned in section 3, summoning spells may include a maximum pressure under which an ectoplasm bubble will manifest. Use of summoning spells in enclosed pressure vessels would be one of the major cases where this limit would come up.
11. Smoke spells
Using our theory of ectoplasm, we can re-derive the mechanics of certain types of DnD conjuration spells. Let’s start with fog or smoke spells: Fog Cloud, Obscuring Mist, Stinking Cloud, etc. All of these spells obscure vision in an area, and generally are dispersed by wind.
Some of these spells claim to be based on mist or fog: water droplets hanging in the air and obscuring vision. I think this is a mistake: water droplets are fairly vulnerable to conditions in the air. Changes in humidity or temperature can rapidly make it impossible for the droplets to hang in the air, and make them either disappear or fall to the ground as rain. Instead, I think smoke is a much better candidate.
Smoke is translucent for the same reasons as fog is: particles hanging in the air of a size that scatters visible light. In the case of smoke, these particles are soot: tiny pieces of unburnt carbon, or small pieces of oxides of whatever was burned. They are going to be much less affected by humidity, and are generally fairly inert, so would not cause problems with biochemistry. Some might note that smoke rises in air: this is not an inherent property of smoke, but rather a consequence of how smoke is normally produced, mainly from fire. Fire is hot and produces hot air, which raises, and brings smoke with it.
12. Fire spells
Many spells create various kinds of fire or explosions. In my view, the simplest way to model them is as a deliberate mixture of some kind of fuel and oxidizer. Fuel can be either ectoplasmic, or permanent; and oxidizer can be either ectoplasmic, permanent, or come from the surrounding environment (i.e. air). Let’s use a carbon-oxygen mixture as an example. In both cases, carbon would need to be preheated to achieve an ignition temperature.
We have some things to consider when picking a mixture type. First one is wherever fuel and oxidizer form a stoichiometric ratio: if there is more fuel or more air than is optimal, then combustion will not be as efficient. Second is wherever environmental oxygen is depleted by combustion: using such a spell indoors would be dangerous. Third is wherever combustion is possible without environmental oxygen (e.g. underwater). Fourth is wherever the reaction leaves any products behind; this means either atomic oxygen (oxidizes anything nearby), atomic carbon (combusts to CO2 in the presence of environmental oxygen), or CO2.
Lifetime for ectoplasmic compounds should be pretty short: there is no need to keep them around for longer than it takes to combust and transfer heat to the environment. Flame can then be seen as a continual process where compounds are summoned, react together, fly up in the jet of plasma, and finally unsnap.

Overall, I prefer ectoplasmic oxygen/ ectoplasmic carbon mixture most.
13. Rundown of spell explanations
Now that I have outlined all the physical mechanics related to summoning matter, I’d like to present a quick rundown of the various summoning spells present in the books. I used sorcerer/wizard spell list as a basis, limited to explicitly conjuration spells, as I think this should offer a good overview of the typical cases. My list of categorized conjuration spells is now available here, and I will probably expand the document with more categories, spells, schools and spell types as time goes on.
I split conjuration spells into six categories. “Temporary conjuration” includes spells where the main effect, or one of the main effects, is conjuration of ectoplasmic matter. “Permanent conjuration” has spells where conjuration of permanent matter is the main effect. “Teleportation/dimensional” spells are ones that deal with what is written on the tin: extradimensional effects. “Telekinesis” spells are ones that primarily or partly just apply some force to something, usually as part of a “helpful minion” effect which manipulates items for you. “Force” spells summon or manipulate objects made out of force walls. Finally, “non-conjuration” refers to all spells that are part of the “conjuration” spell school, but do something completely unrelated to summoning of matter - such as healing - or are just plain weird.
Where appropriate, I added notes regarding my thoughts on those specific spells and their mechanisms of action. Overall, physical/magical laws described in this article cover well over 60% of all conjuration spells in the books. Majority of the rest have to do with teleportation or extradimensionality.
I think this concludes the topics I wanted to cover when it comes to the physics of summoning new matter. Next time I would talk about chemistry and biochemistry of summoned matter - chemical reactions you may see if you burn or otherwise interact with ectoplasmic matter, and what happens inside of your body if you eat a temporary horse. That used to be part of this post, but got large enough I decided to break it off into a separate one.
Post after that would talk about summoning blueprints - schemes that specify what actual objects can be summoned, and that define which atoms get placed where, as well as where a caster could get a blueprint for something as complicated as a whole bear. That article would also try to answer the question of why are summoning spells so limited compared to what should be theoretically possible - for example, why does the Summon Monster spell only allow you to pick out of a small predetermined list of creatures, split into levels by their lethality.
Meanwhile, if you enjoy what I write, you can subscribe to receive updates by email:



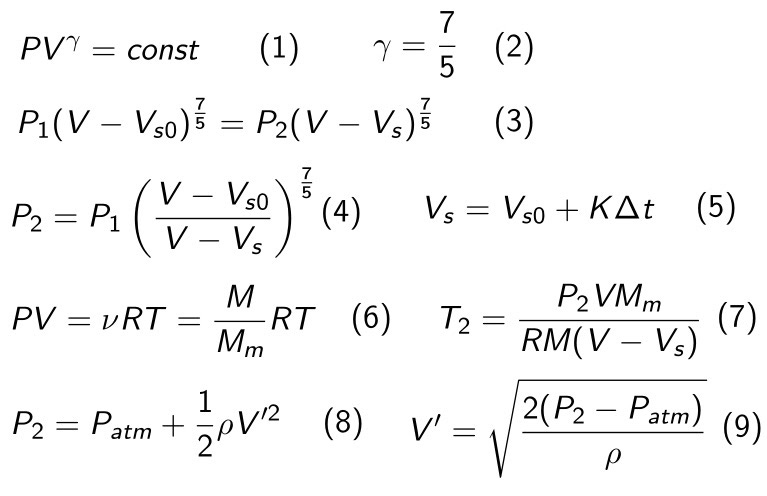

I think the theory behind healing as a conjuration spell is that you're replacing lost flesh or something
There's still potentially a big problem with Disintegrate, although it intersects with HP metaphysics, and I'm not sure if you want to get into that.
If you throw a Disintegrate that deals 60 damage at someone who has 50 HP left, we know what happens: his body unsnaps like a summoned item. But what happens if you throw a 60-point disintegrate at someone with 80 HP left? Your description of unsnapping implicitly seems like an all-or-nothing process. Is "partial unsnapping" a conceptual possibility? Even if it is, the answer can't be "75% of his body unsnaps" because that causes a lot of problems for normal gameplay.
What kind of injuries, if any, would a Disintegrate-survivor experience? What does an "unsnapping energy" do if it doesn't reach the critical threshold?