Reductionist Magic 4: Magical sight and the physics of divination
… or why magical photons are a bad model
Divination as a school of spells in DnD has multiple classic uses. One of them is what I call “scanning spells”. These are spells that turn your caster into a radar by giving them extra vision modes.
It’s pretty natural to think that scanning divination spells would work on the basis of some kind of magical light. Spells like True Seeing, Arcane Sight and Aura Sight have sight in their name. The very word “aura” in spiritualism refers to a “colored emanation” - colored meaning can be perceived with your eyes, because that’s the only thing that perceives colors. Overall, the impression is that these spells let you see some kind of magical light - and thus spells or creatures emitting that light - that was already there, just imperceptible - like one of those studies on mice that let them see infrared.
Unfortunately, this idea simply doesn’t work.
But before we get into this, if you are confused about any terms, make sure to check out the glossary, and if you are looking for other posts, check out the blog map. Finally, if you are reading this in an email, your email client (specifically, gmail) may have cut the post short - sorry for that, but there are a lot of images.
1. Errors of the light model
Let’s talk a bit about how light works. Light, same as any other wave, has three key properties. First of all, it can be absorbed by the material it passes through - this is why you can’t see anything 200 meters below the ocean’s surface. Once you are that deep, water has absorbed so much light that your eyes can’t function. How this absorption happens is complicated, but generally, you will find that it fits an exponential pattern - 1 meter of substance halves the amount of light going through, 2 meters cut it by a factor of 4, 3 by 8, 4 by 16, etc.
Second, it is linear. Linearity has to do with math which isn’t important for us, and in this context simply means that light distributions add up. If you have some set of light sources that would make the target location receive A amount of light, and another set that would make it receive B amount, if you turn both of them on together it will receive A plus B. This also means that if you double the strength of your light source, all the brightness everywhere is doubled.
Third, our space works in a way that makes light decay as 1/r^2, where r is distance to the light source. Imagine that you have a light bulb that is on. We can draw two imaginary spheres around the lamp with radii of 1 and 2 meters; all the photons going through the smaller sphere will also go through the larger one. However, the larger sphere has four times the area - this means that any object 2 meters away will get 1/4 the light of an object 1 meter away.
Light model of divination would then explain the observational results like this: there is some minimum perception limit for your magic light sensor; any light dimmer than that is not seen. Range of scanning spells comes from the 1/r^2 decay, as the light further away than the range of the spell is too dim. Object permeation limit most scanning spells have - “The spell can penetrate barriers, but 1 foot of stone, 1 inch of common metal, a thin sheet of lead, or 3 feet of wood or dirt blocks it” - comes from the absorption property: e.g. 1 foot of stone absorbs so much divination light that anything behind that obstacle is invisible.
Of course, this explanation simply doesn’t work, as it goes contrary to the actual properties of divination spells. Specifically, two of them: limited range, and a sharp break in the permeability of objects based on their thickness.
Let’s draw some diagrams. Say that we have a caster with a divination spell active, and we are doing tests on their vision. Let’s compare what the light model would predict to what actually happens. Upper picture will always have the predictions of the “light” model, and below will be what actually happens in DnD magic. Area in green is the effective vision range of the divination spell, red circle is some test spell we are trying to sense, and blue is various walls.
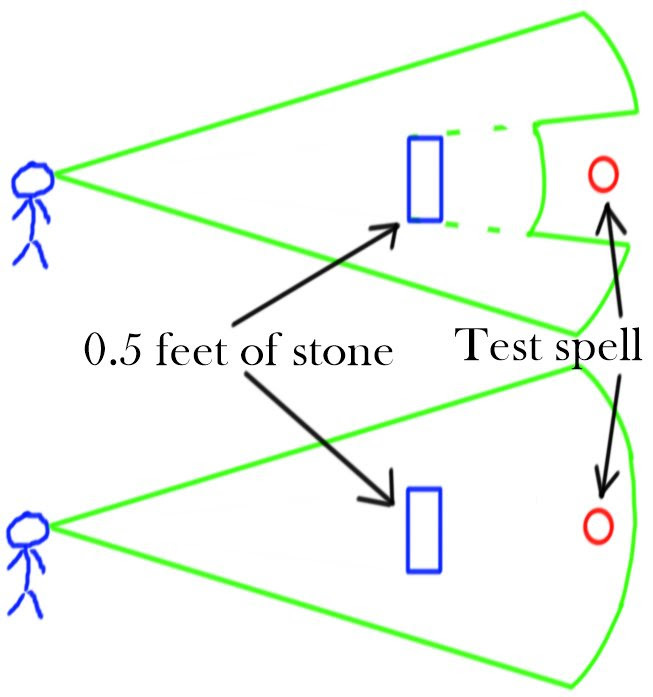
Here, we have only half of a foot of stone. Divination spells in DnD ignore this amount: they are only blocked by 1 foot. Light model, however, can’t ignore it: half a foot of stone has to reduce the range of the spell behind the wall. We therefore have a contradiction: the light model would predict us to not see the test spell, when actually it would be visible.
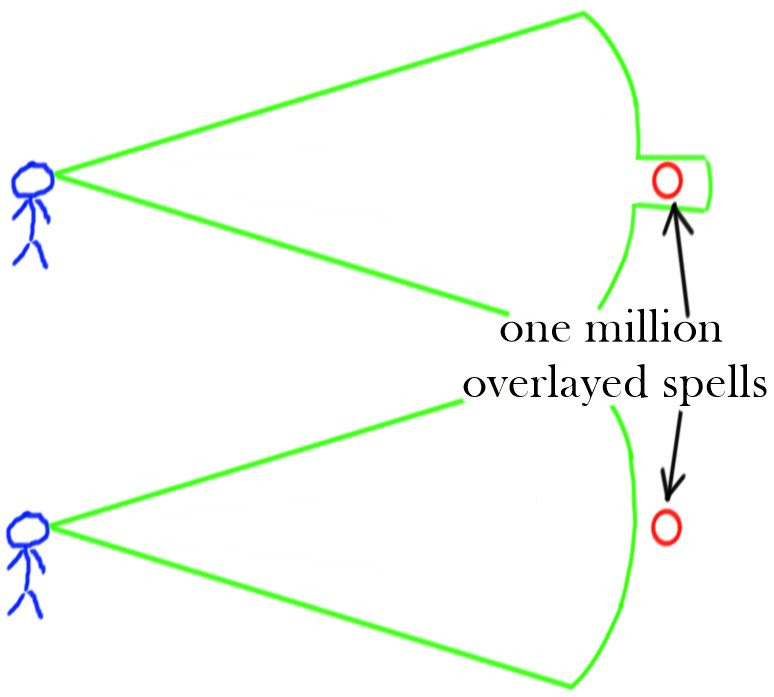
Second issue arises when we consider linearity. Sure, we can claim that effective range of the spell comes from light from the spells dissipating sufficiently by the time it reaches the caster to be invisible. But that sort of calculation only works for one spell. If we cast one million spells in the same spot, light should be a million times brighter, and at that point no amount of absorption or dissipation should prevent us from seeing this massive object just out of our spell range. But that is exactly what happens in DnD magic.
An objection can be made that perhaps the caster is emitting the light, like the radar, and waiting for an “echo”, with spells simply passively reflecting light. Of course, repeating a variant of the above experiment with one million casters all standing in the same spot will disprove this hypothesis too.
As we can see, the light model of divination is fundamentally at odds with how divination works in DnD. What other model can we substitute here?
2. Microspell model of scanning divination
I propose that most divination scanning spells should be treated as a swarm of microspells.
Here, microspell refers to a very small, discrete spell object that travels to a point within the range of the divination spell in a straight line, scans that specific point, and then returns to the caster in order to report on the findings. Microspells suffer damage when going through physical matter; when this damage exceeds a critical threshold, microspell breaks and dissipates. Thicknesses blocking divination spells then refer to the maximum thicknesses a microspell can go through without breaking.
This model is non-linear: 1000 microspells can be absorbed by a plate of lead as easily as 1. It also defined the limited range of the spell as simply the maximum range a microspell can reach before dissipating due to running out of power, or due to being damaged in ways that don’t stack with damage from object penetration.
Now that we have a basic model, we want a formula for deriving damage properties for different materials or their combinations. Let’s start by listing the desiderata we have for this method:
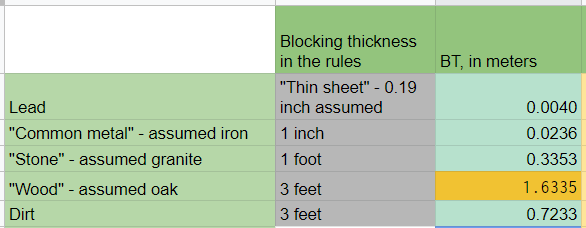
We want it to fit the numbers provided by the rules. Specifically, divination spells should be ~unaffected by air, fall apart after “a thin sheet” of lead, an inch of “common metal”, after about a foot of “stone”, or three feet of “wood” or “dirt”.
Here, one can ask some questions regarding the rules. Specifically, what is a “thin sheet”? What is a “common metal” - steel, copper? I will be assuming that this line is a kind of measurement heuristic as opposed to a strict law. That is to say, when the rules say divination spells are blocked by a “foot of stone”, this means that most kinds of stones block them after about a foot. If an individual stone type blocks divination after 1.5 feet or 0.7 feet, this is fine, as long as the general range falls around the 1 foot mark. The same principle holds for wood and dirt, for there are many kinds of those too. Metals differ a lot in their properties, and so I will be assuming that “common metal” refers to iron. “Thin sheet” will refer to a sheet of about 3 millimetres. I’ll use terms “blocking thickness” and “penetration thickness” interchangeably to refer to the thickness of material that blocks divination.
Air should not affect divination spells because if it did, we would have seen a reduction in the range of the spell when sub-blocking thicknesses of stone (e.g. 0.8 feet) are present. Because no such effect is observed, the damaging effect from the air should clearly be negligible.
Because we want our method for deriving damage properties to be general, it has to rely only on objective physical properties of the materials (constituent atoms, geometry, mass, electrical properties, temperature, any objective magical properties, etc), as opposed to subjective human classifications of those materials - otherwise you get questions like “Is bamboo a wood?”
There are obviously hundreds of different ways to fit a function of all the physical properties of a material to the five data points we have here. In order to constrain that space of possibilities, we can add additional assumptions on top. All of these assumptions are in a real sense arbitrary, and if you make different ones, you will end up with different physics for the divination spells. Most of them make calculation of microspell damage easier in play, so I don’t think people will find them objectionable.
Damage to the microspell does not depend on where along its path it is - wherever it’s closer to the target spot or further away, or wherever it’s flying to the target spot or returning to the caster with the information. Because we can only get experimental results regarding damage throughout the whole path, this assumption is similar to assuming that one-way speed of light is the same in all directions.
Incremental damage from a small thickness of a material doesn’t depend on previous damage to the spell. This, in effect, means that order of the intervening materials doesn’t matter: if we have a wall made out of a lead sheet, a steel sheet, and wooden paneling, total damage to the spell doesn’t change based on the order of those sheets within the wall.
Damage from two equal sheets of an equivalent material is equal. This removes all random damage factors from consideration, making the calculation deterministic. Because we only measure damage on a macro level, this can still mean that on an atomic level the damage is stochastic, as long as that randomness averages out at the macro scale. As a result, all that matters for damage calculations is the material itself, and how much of it was in the way of the spell. Furthermore, together with the previous assumptions, damage from walls of different materials in the way adds up linearly.
Temperature and velocities of the walls relative to the spell don’t play any role in the damage calculations. This is purely because keeping track of temperature is kind of a pain, and also because you don’t want to re-calculate visibility fields for a location depending on the season.
Geometry of the material distributions does not affect the damage calculations, except by changing the effective thickness in the path of the microspell. This is another assumption that simplifies our life: keeping track of geometry for the walls - wherever they are flat or slanted, with bumps or without, etc - would be a lot of extra data tracking and calculation. And while it would affect the visibility for real light (see: lenses), it seems unnecessary for microspells. Thus, the only way for geometry to affect the visibility is through the effect similar to tank armour: sloped walls are thicker.
3. Density-based microspell damage
Now that we have all our assumptions clearly laid out, let’s see what patterns we can fit to the data. The first idea we may have is to base damage calculations on density: lead and metals are denser than stone, and stone is denser than wood and dirt, fitting our progression. Mathematically damage to the microspell then becomes:

In the common, but specific case of there being N distinct homogeneous materials on the path of the spell, we can naturally replace the integral with a sum:
The simplest form f() can take would be a linear function of density:
Unfortunately, this doesn’t work. There is no way to fit a linear function to the data points outlined in the rules, without making large changes to the blocking thickness - for example, changing the blocking thickness of metal to be about a foot instead of an inch. This change is too large for me to stomach. Instead, we can fit a higher order polynomial - as any algebra student should know, a polynomial of N-th power can perfectly fit N+1 points.
In order to fit a polynomial mathematically, I have assumed the following statistics for the materials:

Doing some linear algebra to fit a polynomial to aforementioned data in the rules, we get a graph shown above. It is not satisfactory: there is a strange plato around the 3-4.5 density range, and the polynomial bends towards zero for low densities. This would imply that air is more opaque to divination than dirt, which is obviously bunk.
Looking at the log scale, we can see that the points fall into a vague line:
It is thus natural to try fitting an exponent to the points. Using least squares fit, we get the following:
This is definitely better, but still not satisfactory. Air’s blocking thickness is much too small, making divination spells non-functional. Because of the linear fit in log space, there is no simple way around this. Instead, we can add a point for the air at blocking thickness of 1000 meters, and fit a polynomial of a higher power:


Fit parameters are:
This is a functional fit. It can be used. You can take any material, plug in the density, and get the answer out. There is just one problem: I don’t like it. The fit coefficients we got out are completely arbitrary - even more arbitrary than the thicknesses we used to fit them. And there are six of them! We just introduced six arbitrary constants into our magic system. From an aesthetic perspective, this is terrible!
Furthermore, there is a second, smaller problem. Density is a macroscopic property: atoms don’t have density, they just have mass. To have density, you need to have some small volume over which to average that mass. This means that our definition of microspell damage implicitly has a seventh arbitrary parameter, the volume used to calculate density at a point from the nearby mass. It isn’t expressed as a number, but it’s there.
There is a different way of defining microspell damage that doesn’t have these problems: we can calculate microspell damage the same way as absorption of gamma rays. Ironically, this would bring us somewhat closer to the light model of divination that we have moved away from.
4. Absorption-based microspell damage
First, let’s shortly discuss how absorption works for gamma rays. Let’s say we have a narrow beam of gamma rays, and we want to know how much of it gets through a block of some material to the other side. Specifically, we want to know the intensity (I) of the beam coming out compared to intensity (I_0) coming in. It turns out that this is usually an exponential relationship:
Mass attenuation coefficient is a property of materials, or rather the atoms in them, defining how well they absorb or scatter gamma rays. It depends on the atomic properties, and on the energy of the photons making up the beam: both properties that fit our desiderata for a divination microspell damage model.
If we have two materials in the way, exponents multiply, and so their powers add up.
Taking the log and doing some math, we then get:
This formula then defines our critical level of damage to a microspell, and attenuation weights convert seamlessly into attenuation weights.
In order to make this model fit, we have several variables we can modify:
Effective energy of the spell - what “photon energy” do we use to determine mass attenuation coefficients for our microspell.
Maximum thicknesses of the various materials that let the microspells through.
Critical level of damage.
After it fits, we could simply figure out the attenuation coefficient for our material, plug it into our math, and get the penetration thickness out. Of course, nobody is going to do radiology calculations by hand, so I made a calculator on google sheets. Feel free to make a copy for your own calculations if necessary.
First task is to reduce the number of variables. I decided to use stone as the “lead” material, and every other material as the “follower”: in my calculator, the blocking thickness of stone is taken as a given, and thus defines the level of critical damage. This, in turn, defines blocking thicknesses of other materials. I can then vary the blocking thickness of stone and the energy of the spell, and try to make blocking thicknesses of other materials line up. After doing some optimization, I think the value of 55 KeV and stone thickness of 1.1 foot is the best you can achieve with this method. I also think it lines up pretty well.
Lead gets a thickness of 4 millimetres instead of the target 3. 4 millimetres is still fairly thin, so I think it’s fine.
Metal and stone line up to within 10%.
Dirt is off by about 20%, but in practical game terms 2.3 feet can be rounded up to 3 without much of a loss of generality.
Wood is the only significant outlier - instead of 3 feet, it’s 5.4. This is a large change from the core rules. However, think about when the penetration depth limitations of divination spells come up in play. 3 feet is too thick for a single wall: this is more like three different walls. Therefore, for this limitation to come up, you will need to be looking at some wooden structure that has more than 3 consecutive thick wooden walls within your vision cone, and you have to be interested in what is on the other side of all these walls. This is going to be a pretty rare circumstance. Most likely, if you are trying to look through 3 feet of wood, you are stuck in a warehouse that stores giant piles of wood: in which case wherever it’s 3 feet or five feet, the difference will be minor.
Overall, I prefer this method of calculating divination spell penetration depths to the one based on density. This may or may not be because of how much effort I put into the calculator, but that’s the method I will be sticking with for the rest of this series. It does have a downside of being harder to use for a new material, though, because you have to enter it’s elemental composition into a table in the calculator.
5. Multiple materials
Regardless of which method you choose, there is an easy way to do math for multiple materials in the way of the spell. Simply put, fractional drains of the damage capacity add up.
Initially, the spell has 100% of capacity. Then it goes through, for example, 10 centimeters of granite. Granite has a maximum penetration depth of 30cm, meaning 10 centimeters is 33% (1/3) of that - so the spell has exhausted 33% of capacity and has 67% left. If it then goes through 1.5 mm of lead (50% of max PD), it will only have 17% left. Trying to go through wood after this will leave it only able to go through 17% of 1.2 meters - about 20cm. Thickness numbers are taken from the density method of calculation.
I leave it as an exercise to the reader to prove this mathematically.
6. Comparison of calculation methods and implications of material penetration depths
Of course, we have to compare the calculation methods in terms of what blocking depths you get for different materials. This will also give us a broad overview of different material types.

What do we see here? Well, honestly, the two calculation methods give pretty similar results. Differences of up to 20% are small enough you can ignore them completely in normal play. It’s going to be a pretty rare player party that is going to care about e.g. sand having a blocking weight of 66 as opposed to 70 centimetres. You can thus pick whichever method you like best.
One notable exception is tin. Tin is a moderately common metal (rarer than copper or lead, much more common than gold or silver), and is a key component in making bronze (common bronze is an alloy of 1/8 tin 7/8 copper by weight; metals other than tin can also be used, but I think tin was and is more common), is easy to work (melting point of only ~200C), and was well known historically (e.g. it’s a common roof shingle material). It also happens to have a fairly high atomic number, which makes it an excellent absorber of gamma rays at our picked microspell energy. Given it’s low density, it thus becomes a better shielding material for movable containers than lead (at least for this energy range. It falls behind quickly for higher energies, which is why it’s not used to block gamma rays in real life).
I think this is fine. Given it’s relative rarity, lead should still be the economically optimal shielding material, and thus will be used for shielding whenever shielding is necessary. Reduction in weight for movable containers is likewise not significant: you are still looking at several kilos of metal weight, even for relatively modest boxes. This means that if you are running a pre-written adventure where divination blocking is common, you shouldn’t need to change much.
Given we are discussing movable containers, it’s worthwhile to talk about the thickness I picked for lead. 3 mm somewhat stretches the believability of what a “thin sheet” might be - it’s actually relatively thick. Why this number? Well, the truth is that I worked backwards: first calculated what kind of values you can work with, and then wrote them at the top as initial assumptions. The main problem is that using gamma ray absorption locks you into a fairly small set of values - it’s actually kinda lucky we managed to get the numbers this close to what is written in the rules. For polynomial density fits, the coefficients - and thus the shape of the polynomial - depend very strongly on where exactly the points are. For example, here is how the polynomial looks like when desired lead thickness is halved to 1.5 mm:

Yeah, that’s not great. You could add more points to make it fit a good shape, but I wasn’t motivated to do so.
This does mean that movable containers that block divination become kinda heavy, because 3-4 mm of lead is actually a lot of lead. For example, a plate of lead the size of an A4 paper 4 mm thick weighs 2.81 kilos. To make a paper folder that would hide the documents inside, you would thus need more than 5 kilos of lead (one plate for the front, one for the back). I am not sure whether any pre-written campaign or setting material uses such movable divination blockers as a plot point, but if it does, this may be a fairly large change.
Personally, I think this is (coincidentally) a great change to make. It fairly naturally explains why people don’t just use lead all over the place to block divination, even if they have the economic means for it - it’s just uncomfortably heavy. Putting lead shielding on all your magical items becomes much less attractive if that means lugging tens of kilos of lead around with you (though a paranoid player may do so regardless).
Another change that arises from trying to use a reductionist approach to divination shielding is that water now explicitly shields from divination, and is actually fairly good at it - about as good as wood. Blocking length of about a meter means that even shallow lakes can hide all sorts of things, despite being easily navigable by humans and monsters. This turns sources of water into excellent ambush spots - anyone wandering close and relying on divination to warn them of threats will be fooled. It further makes any underwater adventures highly dangerous, as most vision modes are effectively nerfed. I think this is fine - water-specific sensory spells can be designed for those cases, ones relying on sound or light instead of magic. Ambushing possibilities of water likewise seem interesting to me, compared to the alternative.
7. Density measurement and the magical TSA
Because of how scanning divination spells work now, there is a neat application of these spells with widespread effects. Regardless of which calculation method you choose, more matter means divination is more likely to be blocked: we can thus measure density of objects by seeing if they block divination or not.
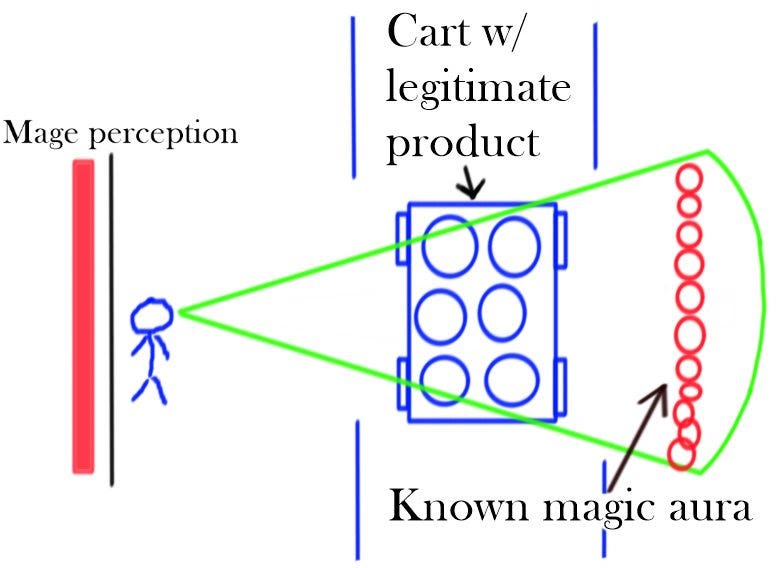
In order to set this up, we need three things. First, we need a mage with an active divination spell: Detect Magic would work fine. Second, we need something that that detection spell can see: in case of Detect Magic, an active spell aura, that our mage knows about in advance. Finally, we need to put a questionable object in between the mage and the active spell.
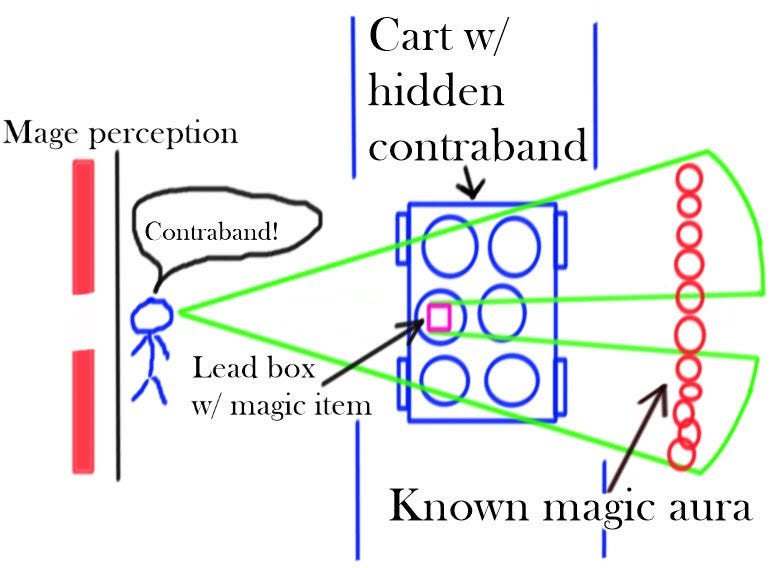
If the suspicious object has weight and materials such that it doesn’t block divination, then the mage will see the entire magic aura. On the other hand, if some part of the object blocks divination, then the mage will not see the magic aura in a corresponding spot: as a result, they can detect spots of strange density within the scanned object. This method can be used to detect smuggled magic items, even when the aura of the magic item can’t be seen: suspicious amount of shielding will show up on the test. Likewise, it’s feasible to detect other kinds of contraband that differ strongly from the expected surrounding material (e.g. iron weapons within the wooden base of a cart).
As described above, the method can only give binary information: either the sight is blocked or not, either the total thickness is above the 100% damage cutoff or not. In order to get more information out of the scan, sheets of tin with sub-blocking thicknesses can be used. Because of the stacking rule (see section 5) putting these sheets in front of the scanner can allow the mage to detect more fine-grained density variations. For example, a tin sheet 10% of the blocking thickness can allow the mage to see the difference between an object 91% thick (101% together with the sheet -> sight is blocked) and 89% (does not block sight). There are many ways to do this, though I am partial to glasses similar to the ones used by optometrists, with exchangeable “lenses”.

8. Consequences coming from the tank armor effect
Because scanning divination spells depend on the thickness of the material to determine if your vision is blocked, they would naturally be under the influence of the “tank armor” effect. This is simply an observation that a plate of a certain thickness is effectively thicker if you angle it relative to an incoming line. Because of this, when looking at a wall of a sub-maximum penetration thickness, divination spells will not be able to see through the entire wall. There would instead be a circular “window” in the wall, opposite of the caster: within the window the wall would be transparent, and outside it would be opaque, because the increasing sight angle relative to the wall will increase the wall thickness.
However, when it comes to divination, this effect is honestly not too important. Consider someone who is standing D meters away from the wall: how big of a window would they see?
Doing some calculations, we can describe the radius of the window as distance to the wall, times a multiplier. We can see that for even fairly significant wall thicknesses (90%) we get a window radius that is comparable to the distance (50%) - meaning, if you were 3 meters away from the wall, the transparent window would be 1.5 meters in radius. Because of how large this window is, in the vast majority of the circumstances, you can simply treat the entire wall as being transparent.
Conclusion
Overall, I think this is a pretty significant improvement in the consistency of the scanning divination effects. This method avoids all arguments about whether something is “stone” or not, or “wood” or not, deals flawlessly with material mixtures of all kinds, and can be trivially modified to account for spells that go through more (or less) material, or have an entirely different distribution of penetration thicknesses for key materials. I hope the tools I developed here, and the explanations behind my thinking, could be useful to some people in their designs of TTRPG settings. Meanwhile, if you enjoy what I write, you can subscribe to receive updates by email:
Licenses
Sloped tank armor picture is taken from here by Balcer~commonswiki, and is licensed under CC BY-SA 3.0.
Sources
https://www.nist.gov/pml/x-ray-mass-attenuation-coefficients
https://www.researchgate.net/figure/Elemental-composition-of-birch-wood-samples_tbl1_336004115
https://www.inchcalculator.com/lumber-weight-calculator
https://en.wikipedia.org/wiki/Sun
https://en.wikipedia.org/wiki/Granite
https://www.researchgate.net/figure/Chemical-composition-of-glass-wastes_tbl1_281106141
https://chemistry.stackexchange.com/questions/139386/density-range-of-table-salt















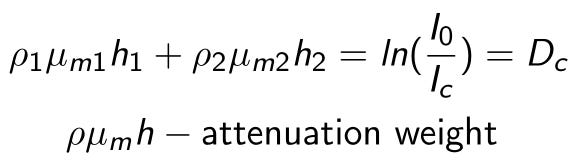


I like the drain adding up idea. A great read!